PMM 核心

PMM 本质上是利用智能合约求解一个积分和两个二次方程的算法。

价格曲线积分

对于交易者来说，最重要的是平均成交价格。平均交易价格是边际价格的积分 $P_{margin}$。我们用 base token 短缺的情况举个例子：

$\Delta Q =\int^{B_2}_{B_1}P_{margin}dB$

$= \int^{B_2}_{B_1}(1-k)i+i(B_0/B)^2kdB$

$= i(B_2-B_1)*(1-k+k\frac{B_0^2}{B_1B_2})$

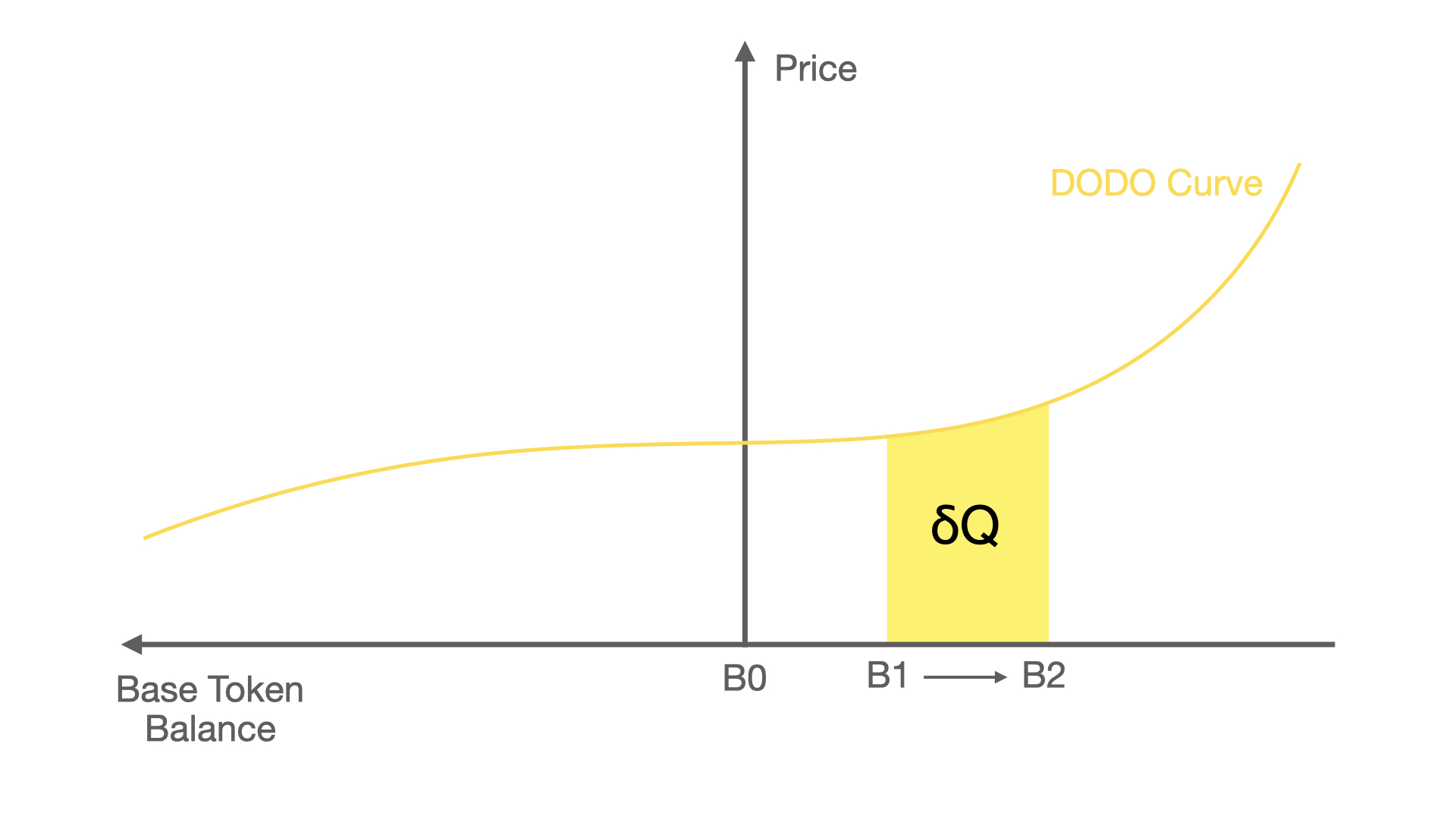
这个公式告诉交易者如果他们想买 $B_1-B_2$ 数量的 base token，他们需要支付多少。

将上边的公式做个变形，我们就可以而得出平均成交价为： $P=\frac{\Delta Q}{B_2-B_1}=i*(1-k+k\frac{B_0^2}{B_1B_2})$

平均成交价只取决于交易前后系统的状态，所以买卖的价格计算公式都是一样的 ———— 求边际价格的积分 $P_{margin}$。

求解交易的二次方程

在没有一般损失的情况下，当 quote token 短缺的时候，积分会变成：

$\Delta B = \frac{1}{i}(Q_2-Q_1)*(1-k+k\frac{Q_0^2}{Q_1Q_2})$

交易者想要交易的数量，比如 $\Delta B 已知，我们来推导下 quote token 短缺时的价格。

$\Delta B, Q_0, Q_1$ 已知，我们可以通过推导二次方程得出 $Q_2$ ，把二次方程做个变形可以得到：

$(1-k)Q_2^2+(\frac{kQ_0^2}{Q_1}-Q_1+kQ_1-i\Delta B)Q_2-kQ_0^2=0$

$let \ a=1-k, \ b=\frac{kQ_0^2}{Q_1}-Q_1+kQ_1-i\Delta B, \ c=-kQ_0^2$

因为 $Q_2>=0$, 我们舍掉符号，得出：

$Q_2=\frac{-b+\sqrt{b^2-4ac}}{2a}$

可以证明：

• 当 $\Delta B>0$ 时, $Q_2>Q_1$; 交易者想买 base token 时，需要支付 $Q_2-Q_1$
• 当 $\Delta B<0$ 时, $Q_2<Q_1$; 交易者想出售 base token 时，会收到 $Q_1-Q_2$
• 当 $\Delta B=0$ 时, $Q_2=Q_1$.

同时DODO V2，在以上的方程计算上，着重验证了k=0, 以及k=1 的特殊情况，以支持恒定价格卖币以及标准AMM的bonding curve。

求解回归目标的二次方程

当系统处于不平衡状态时，预言机的价格变化会带来盈利或亏损。举个例子，假设当前 base token 短缺，预言机价格上涨。此时，多余的 quote token 显然不能买回足够的 base token 让资产池数量回归到平衡状态。那么充入 base token 的做市商就亏损。相反，如果预言机价格下跌，多余的 quote token 可以买会足够多的 base token 让资产池回归平衡状态同时还有富裕，那么充入 base token 的做市商就会盈利。

总之，回归目标受预言机价格影响，我们可以通过下面的公式推导当预言机价格为某一个价格时的回归目标：

Given $\Delta Q = i(B_2-B_1)*(1-k+k\frac{B_0^2}{B_1B_2})$

因为进行回归计算，$B_2=B_0$，将公式做个变形

$\frac{k}{B_1}B_0^2+(1-2k)B_0-[(1-k)B_1+\frac{\Delta Q}{i}] = 0$

消除负根，得出

$B_0=B_1+B_1\frac{\sqrt{1+\frac{4k\Delta Q}{B_1 i}}-1}{2k}$

这种情况下， $\Delta Q=Q-Q_0$。可以证明， $\Delta Q \ge 0$ 时, $B_0\ge B_1$.

这个结论非常重要，因为它确保了 base token 和 quote token 不会同时大于或小于回归目标。这意味着 PMM 只会出现核心观念中提到的三个状态。

同样，quote token 的回归目标推导公式为：

$Q_0=Q_1+Q_1*\frac{\sqrt{1+\frac{4k\Delta B i}{Q_1}}-1}{2k}$

其他

这一节会介绍 PMM 算法相关的其他数学运算。

交易

如上文所述，回归目标取决于预言机价格，价格曲线又取决于回归目标。所以每笔交易中我们都需要提前计算回归目标来固定价格曲线。

另外，由于 PMM 给出的价格曲线是分段的，所以如果一笔交易涉及到不同的状态，（比如当 base token 短缺时交易者出售巨量的 base token，系统状态会有 base token 短缺变为 quote token 短缺），价格需要分段进行计算。

请注意，这个计算需要非常高的准确度，智能合约为三种状态提供了六种交易功能。你可以在这里找到跨状态交易的逻辑。

充值

当资产处于短缺的状态时，充值或提取会影响价格曲线。这就要求我们要谨慎地处理充值和提取来保证资产池的可持续性和公平性。

我们来分析下当 base token 短缺时，做市商要提取代币会发生什么。

根据 $B_0$ 的推导公式，得出： $B_0=B_1+B_1*\frac{\sqrt{1+\frac{4k\Delta Q}{B_1 i}}-1}{2k}$

当做市商存入 $b$ 个 base token 时， $B_1$ 上涨 $b$， $B_0$ 上涨幅度更大。这就意味着这笔充值会让所有充入 base token 的做市商获利，这是因为这笔充值会让价格曲线变平滑，同样数量的 $\Delta Q$ 可以购买更多的 base token.

这种情况下，做市商一旦充入资金，做市商就会盈利，这被称为充值奖励，奖励主要是由让系统偏离平衡状态的交易者支付的。

注意：充值奖励并不是无风险的套利交易机会。

提取

同样，在做市商提取 $b$ 个 base token 后，$B_1$ 下降 $b$，$B_0$ 下降幅度更大。这笔提取会让所有的做市商遭受亏损，这是因为这笔提取让价格曲线变的更加陡，多余的 quote token 买不回同样多的 base token。

PMM 算法要求在这种情况下，提取需要支付一定的手续费。手续费等于这笔引起的做市商的亏损总和。这笔手续费将会被分配给还未提取的做市商。

考虑到上面我们提到的充值奖励，如果做市商在充值后立即提取，提取的手续费会大于充值奖励，从而杜绝了无风险套利。

值得注意的是，只有当系统严重偏离平衡状态并且充值或提取的数量很大时，PMM 才会发放充值奖励或收取提取手续费。一般情况，交易者不用关注这两部分。当然，我们也非常欢迎交易者在系统偏离平衡状态时充值赚取奖励，等系统平衡后提取避免被收取手续费。